Adding A Control To A Quantum-Gate
The power of entanglement
In quantum computing, we use quantum transformation gates to change the states the qubits are in.
For example, the X-gate (NOT-gate) switches the probability amplitudes of a qubit. It turns |0⟩ into |1⟩ and vice versa. When we entangle two qubits, we can refine the behavior of the X-gate. The controlled X-gate (CNOT-gate) switches the amplitude of a qubit (the controlled qubit) only if another qubit (the control qubit) is in state |1⟩.
But the effect we want to apply on the controlled qubit is not limited to switching its amplitude. The CNOT-gate lets us easily turn any qubit transformation gate, let’s call it U, into a controlled one.
Besides the CNOT-gate, there are two more things we need. The first thing is to split the gate U into halves. We must find a gate — let’s call it V that, if applied twice, results in the desired overall transformation gate U. We can say V⋅V⋅|υ⟩=U⋅|υ⟩. In short, V⋅V=U or V=√U. Thus, V is the square root of U.
The second thing is to create a gate that reverts the effect of gate V. Usually, this is the transpose of the gate’s transformation matrix. The transpose (VT) of a matrix is the original matrix V flipped over its diagonal (from top-left to bottom-right).
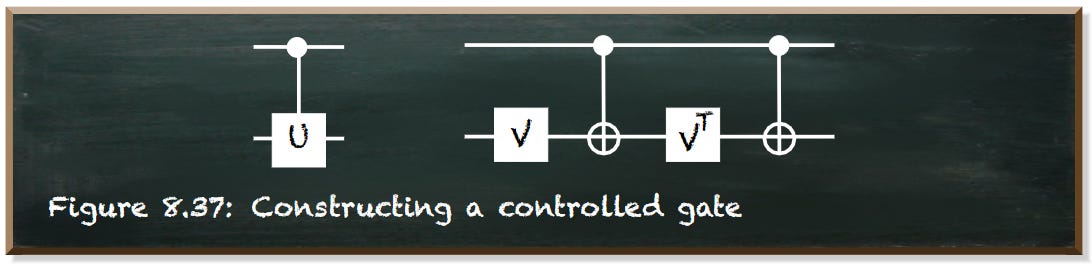
The following figure depicts how we control an arbitrary gate U.
First, we apply the V-gate on the controlled qubit. Thus, we completed half of the U-gate. Then, we entangle the qubits. Thus, the controlled qubit flips its state. But it flips it only if the control qubit is in state |1⟩.
When we now apply the transpose matrix VT, it reverts the effect of V. But only if the control qubit is |0⟩ because in this case, the CNOT-gate does not have any effect.
By contrast, if the control qubit is in state |1⟩ the CNOT-gate flipped the state of the controlled qubit. It is in the exact opposite state. When we now apply the transposed VT-gate, we apply the exact opposite of V once again. Because VT is the opposite of V. Essentially, if the control qubit is in state |1⟩ we applied NOT-V⋅V — or NOT-U.
The final CNOT-gate turns the state NOT-U into U. But again, only if the control qubit is in state |1⟩.
Maybe a single control qubit is not enough? Maybe we want two control qubits.