How To Implement Quantum Error Mitigation With Qiskit And Mitiq

Learn how to implement the Clifford Data Regression

You can read this post on Medium.

Quantum error mitigation is paramount to tap the potential of quantum computing today. First, the qubits we have today suffer from noise in the environment ultimately destroying any meaningful computation. Second, by no means, we don’t have enough physical qubits to bundle them into fault-tolerant logical qubits.

The best we can do today is to reduce the impact the noise has on the computation. That is what quantum error mitigation is about.

Recently, IBM announced its second Quantum Science Prize. They’re looking for a solution to a quantum simulation problem. They want us to use Trotterization to simulate a 3-particle Heisenberg model Hamiltonian. Yet, the main challenge is to cope with the inevitable noise because they want us to solve the problem on their 7-qubit Jakarta system.

But before we can solve this problem on the real quantum computer, let’s first have a look at how we can implement a quantum error mitigation method with Qiskit at all. In my previous post, I introduced the Clifford Data Regression (CDR) method developed by P. Czarnik et al., Error mitigation with Clifford quantum-circuit data, Quantum 5, 592 (2021). In this recent and promising error mitigation method, we create a machine learning model that we can use to predict and mitigate the noise by using the data from quantum circuits that we can simulate classically.

We use Qiskit, the IBM quantum development library, and Mitiq, a Python toolkit for implementing error mitigation techniques on quantum computers.

Mitiq provides an API for the CDR method and they integrate well with Qiskit. So, it should be a piece of cake to get this working, no?

Let’s first have a look at Mitiq’s introduction to CDR. At first sight, they clearly describe what we need to do. It is a four-step procedure:

1. Define a quantum circuit

2. Define an executor

3. Observable

4. (Near-Clifford) Simulator

However, when we look a little closer, we see that their example uses Google’s Cirq library.

So, we need to adapt the code to the Qiskit API.

Define A Quantum Circuit

The quantum circuit we need to define represents the problem we aim to solve, such as the Hamiltonian simulation IBM asks us for. Yet, we stick with the example Mitiq provides. This is a two-qubit circuit that only consists of Clifford gates and rotations around the Z-axis (𝑅𝑍). Clifford gates are easy to simulate on a classical computer — a precondition for the CDR method.

The following listing depicts the adaption of the quantum circuit to Qiskit.

# 1. Define a quantum circuit
from qiskit import QuantumCircuit

def get_circuit():
    qc = QuantumCircuit(2)

    # CDR works better if the circuit is not too short. So we increase its depth.
    for i in range(5): 
        qc.h(0) # Clifford
        qc.h(1) # Clifford
        qc.rz(1.75, 0)
        qc.rz(2.31, 1)
        qc.cx(0,1) # Clifford
        qc.rz(-1.17, 1)
        qc.rz(3.23, 0)
        qc.rx(pi/2, 0) # Clifford
        qc.rx(pi/2, 1) # Clifford

    # We need to measure the qubits
    qc.measure_all()
    return qc

Do you notice anything? Right, the function returns a float, not a density matrix. Furthermore, the function requires an obs parameter. This is an observable as a NumPy array. We would create the observable in the next step. So, let's postpone the definition of the executor for a second.

Observable

Generally, the observable is something we can measure. But, let's not get into the physical details too much. Rather, let's look at it from a conceptual perspective.

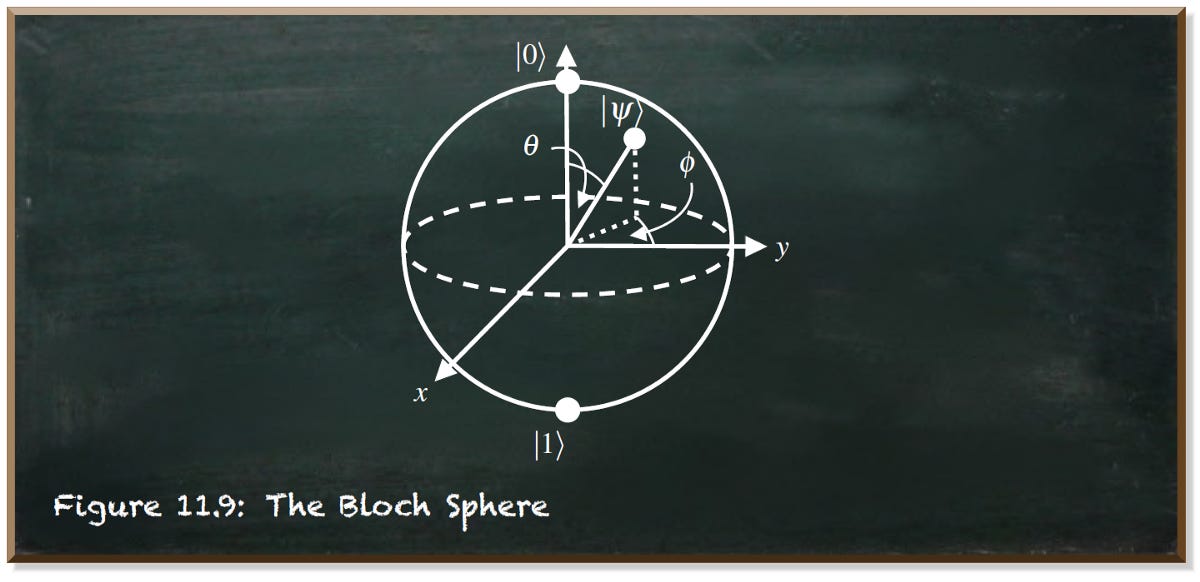
A qubit is a two-dimensional system as depicted in the following image. The poles of the visualization depict the basis states |0⟩ and |1⟩. The arrow is the quantum state vector. The proximities to the poles (the basis states) denote the amplitudes whose squares are the probabilities of measuring the qubit as either 0 or 1. Simply put, the closer the quantum state vector is to the basis state |1⟩ the higher the probability of measuring the qubit as a 1.

So far so good. Yet, the amplitudes of the quantum state are complex numbers. A complex number is a two-dimensional number with a real part and an imaginary part as shown in the following figure.

This effectively turns the qubit into a three-dimensional construct that we usually represent as the Bloch Sphere. Still, the proximities to the poles determine the measurement probabilities.

A sphere is homogeneous. There’s no special point at all. The definition of the poles to represent |0⟩ and |1⟩ is arbitrary. We could define two other opposing points on the sphere’s surface and ask for the probabilities of measuring the qubit as either one. The following figure depicts two such points.

Practically, this is an observable that we specify by a rotation of the overall sphere. The points that end up at the poles of the rotated sphere become the measurement we obtain from looking at the qubit.

Mitiq provides an API to specify an observable. It takes a list of PauliStrings. These denote the rotations of the Bloch Sphere. In the Mitiq example, we have two qubits. The first PauliString applies Z-gates on both qubits (flipping around the Z-axis). The second PauliString applies a rotation around the X-axis on the first qubit by -1.75 (that is a little more than half the circle that would equal 𝜋 (around 3.14).

When we look at the observable, we can see that it outputs the compound rotation.

from mitiq import Observable, PauliString

obs = Observable(PauliString("ZZ"), PauliString("X", coeff=-1.75))
print(obs)

Z(0)*Z(1) + (-1.75+0j)*X(0)

So, with the observable at our disposal, let's return to the executor.

Define An Executor - Revisited

The execute_with_noise_and_shots function requires the observable as a NumPy array. We get this representation by calling the matrix function of the observable object.

Next, we need to specify a noise_model. The noise_model tells the simulator what kind of noise to add to the simulation.

Qiskit provides the noise package to create a custom noise_model. We use it to add errors on single-qubit and two-qubit gates with a certain probability. This means that whenever we apply a gate of a specific kind, we will end up with a destroyed qubit state with the specified probability.

# 2. Define an executor
from mitiq.interface.mitiq_qiskit import qiskit_utils
from qiskit import QuantumCircuit, execute, Aer
import qiskit.providers.aer.noise as noise

# Error probabilities
prob_1 = 0.005  # 1-qubit gate
prob_2 = 0.01   # 2-qubit gate

# Depolarizing quantum errors
error_1 = noise.depolarizing_error(prob_1, 1)
error_2 = noise.depolarizing_error(prob_2, 2)

# Add errors to noise model
noise_model = noise.NoiseModel()
noise_model.add_all_qubit_quantum_error(error_1, ['u1', 'u2', 'u3'])
noise_model.add_all_qubit_quantum_error(error_2, ['cx'])

def sim_noise(qc):
    return qiskit_utils.execute_with_shots_and_noise(qc, obs.matrix(), noise_model, 4096)

Finally, we need to specify the number of shots we want to run the circuit. Anything beyond 1000 shots should work fine.

(Near-Clifford) Simulator

The final component is a noise-free simulator. It is almost similar to the executor. The only difference is that it should not have any noise. We can simply use the execute_with_shots function.

def sim(qc):
    return qiskit_utils.execute_with_shots(qc, obs.matrix(), 4096)

Run CDR

We're ready to run the CDR. We can use the rest of the example code as it is. We only need to plug in the functions we created.

We first compute the noiseless result.

ideal_measurement = obs.expectation(get_circuit(), sim).real
print("ideal_measurement = ",ideal_measurement)

ideal_measurement =  0.6259272372946627

Then, we compute the unmitigated noisy result.

unmitigated_measurement = obs.expectation(get_circuit(), sim_noise).real
print("unmitigated_measurement = ", unmitigated_measurement)

unmitigated_measurement =  0.48027121352169094

Next, we calculate the mitigated result from CDR.

from mitiq import cdr

mitigated_measurement = cdr.execute_with_cdr(
    get_circuit(),
    sim_noise,
    observable=obs.matrix(),
    simulator=sim,
    seed=0,
).real
print("mitigated_measurement = ", mitigated_measurement)

mitigated_measurement =  0.6076182171631638

Finally, we compare the results.

error_unmitigated = abs(unmitigated_measurement-ideal_measurement)
error_mitigated = abs(mitigated_measurement-ideal_measurement)

print("Error (unmitigated):", error_unmitigated)
print("Error (mitigated with CDR):", error_mitigated)

print("Relative error (unmitigated):", (error_unmitigated/ideal_measurement))
print("Relative error (mitigated with CDR):", error_mitigated/ideal_measurement)

print(f"Error reduction with CDR: {(error_unmitigated-error_mitigated)/error_unmitigated :.1%}.")

Error (unmitigated): 0.14565602377297177
Error (mitigated with CDR): 0.018309020131498932
Relative error (unmitigated): 0.23270440251572316
Relative error (mitigated with CDR): 0.029251035968066913
Error reduction with CDR: 87.4%.

A look at the results shows that CDR mitigates almost 90% of the errors that result from the noise.

Mitiq helped us to use CDR almost out of the box. We did not have to bother with the implementation of it at all. However, preparing the code to work with the API is a little bit tricky because the example seems to be outdated.

You're interested in quantum computing and machine learning...

...But you don't know how to get started?